Dynamical Grooming meets LHC data

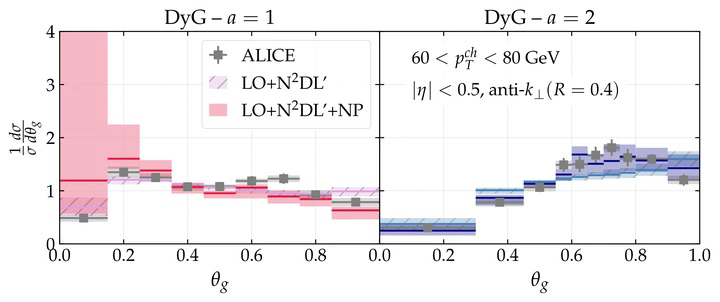
In this work, we analyse the all-orders resummation structure of the momentum sharing fraction, $z_g$, opening angle, $\theta_g$, and relative transverse momentum, $k_{t,g}$, of the splitting tagged by the Dynamical Grooming procedure in hadronic collisions. We demonstrate that their resummation does non-exponentiate and it is free of clustering logarithms. Then, we analytically compute the probability distributions of ($z_g,\theta_g,k_{t,g}$) up to next-to-next-to-double logarithm accuracy (NNDL) in the narrow jet limit, including a matching to leading order in $\alpha_s$. On the phenomenological side, we perform an analytic-to-parton level comparison with Pythia and Herwig. We find that differences between the analytic and the Monte-Carlo results are dominated by the infra-red regulator of the parton shower. Further, we present the first analytic comparison to preliminary ALICE data and highlight the role of non-perturbative corrections in such low-$p_T$ regime. Once the analytic result is corrected by a phenomenologically determined non-perturbative factor, we find very good agreement with the data.

JHEP 07 (2021) 020